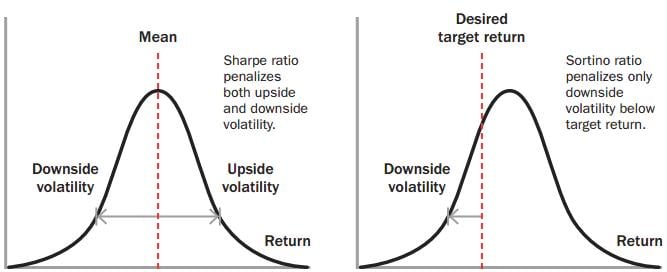
Sortino Ratio – a ‘Sharpe’ Ratio?
In several ways, the Sortino ratio is an absolute choice as compared to the Sharpe ratio, especially when you tend to measure and compare the delivery of managers whose programs showcase positively-skewed return distributions. The Sortino ratio is an adjustment to the original Sharpe ratio simply by using a downside deviation instead of a standard deviation as the risk measure component – i.e., only those returns lying below a user specified threshold (“Desired Target Return”) or a required rate of return should be considered risky.
Ever heard about sortino ratio in stock market, To know more check out our blog on it!
The Sortino ratio, S, is defined as:
S = (R – T) / TDD
Where,
• R is the average period return;
• T is the required rate of return for an investment strategy, which is under consideration (originally T was the Minimum Acceptable Return.
• TDD is the target downside deviation.
The Target Downside Deviation is defined as the root-mean-square, of the deviations of the Realized Return’s under-performance from the target return, where all returns above the target return are treated as underperformance. Mathematically:
Target Downside Deviation =
Where,
Xi = ith return
N = total number of returns
T = target return
The equation for TDD is very similar to the definition of standard deviation:
Standard Deviation =
Where,
Xi = ith return
N = total number of returns
u = average of all Xi returns
The differences however are:
1) In the Target Downside Deviation calculation, the deviations of Xi of the user preset-target return are measured, however, in the Standard Deviation calculation, the deviations of Xi from the average of all Xi is measured.
2) In the Target Downside Deviation calculation, all Xi beyond the target return are set to zero, however, these zeros are still included in the summation. The calculation for the Standard Deviation has no Min () function.
Standard deviation is the measure of dispersion of data around its mean. Target Downside Deviation is a measure of dispersion of data below some user-preset threshold return, with all the above-target returns treated as under-performance.
The Calculation
In this example, we are calculating the annual Sortino ratio for a hypothetical CTA with positive skew with the following set of annual returns:
Annual Returns: 4%, 2%, –2%, 36%, 12%,–4%, 2%, –2%
Target Return: 0%
Although, in the above example we are using a target return of 0%, any value can be selected depending on the application, i.e., a forward trading system developer can compare a different trading systems versus a Pension Fund Manager with a target to achieve 16% annual returns. Using a different target return would result in a completely different value for the Target Downside Deviation. In case you are using the Sortino ratio to compare the alpha component or trading systems, you ought to be consistent in using the same target return value.
Firstly, let’s calculate the numerator of the Sortino ratio – the average period return minus the target return:
Average annual return – Target return = 6.50% – 0% = 6.50%
Secondly, we would calculate the Target Downside Deviation:
1) For each of the data attribute, you need to calculate the difference between that data point and the target level. For those data points above the threshold, set the difference to 0%. The result of this step is the under-performance data-set.
min(0, 4% – 0%) = 0%
min(0, 2% – 0%) = 0%
min(0, –2% – 0%) = –2%
min(0, 36% – 0%) = 0%
min(0, 16% – 0%) = 0%
min(0, –4% – 0%) = –4%
min(0, 2% – 0%) = 0%
min(0, –2% – 0% ) = –2%
2) Following the above, you need to calculate the square of each of the values in the under-performance data attributes.
0% ^ 2 = 0%
0% ^ 2 = 0%
–2% ^ 2 = 0.04%
0% ^ 2 = 0%
0% ^ 2 = 0%
–4% ^ 2 = 0.16%
0% ^ 2 = 0%
–2% ^ 2 = 0.04%
3) Next, you should calculate the mean of all squared differences. It’s important to make a note that we do not remove the 0% values.
Average = (0% + 0% + 0.04% + 0% + 0% + 0.16% + 0% + 0.04%) / 8 = 0.03%
4) Now you should take the square root of the average determined in Step 3. This is the target downside deviation
used in the denominator of the Sortino ratio.
Target Downside Deviation = Square root of 0.03% = 0.173%
Here, we calculate the Sortino ratio:
Sortino Ratio = 6.5% / 0.173% = 3.75
This is a very score and highly indicative of the return string from which we calculated it. Calculating the Sharpe ratio on the same set of returns would have yielded us 0.52, a mediocre one that indicates more volatility by penalizing the outsized positive returns. To conclude that the Sortino Ratio is a better ratio as against the rest is definitely not an overstatement.
Click here To Open Lowest Brokerage Trading Account
[email-subscribers namefield=”NO” desc=”Subscribe now to get latest updates!” group=”Public”]











[…] Also Read : Sortino Ratio – a ‘Sharpe’ Ratio? […]
Too arithmetical n bookish with hardly any impact on trading or investing in practical trading or investing world !!